JS输出杨辉三角(带解析) 图片看不了?点击切换HTTP 返回上层
杨辉三角是一个经典的编程案例,它揭示了多次放二项式展开后各项系数的分布规律。简单描述,就是每行开头和结尾的数字为 1,出第一行外,每个数都等于它上方两数之和,如图所示。
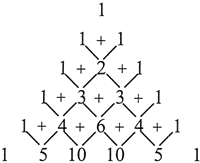
完成算法设计之后就可以设计输出数表。如图所示。
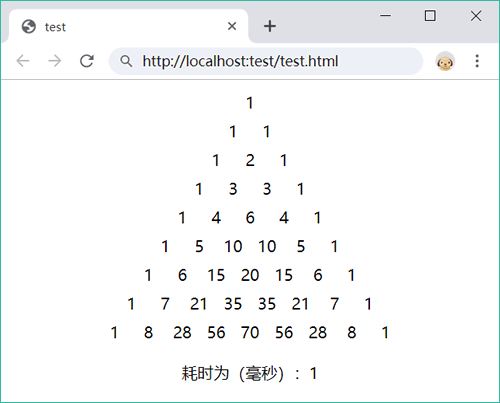

设计思路
定义两个数组,数组 1 为上一行数字列表,为已知数组;数组 2 为下一行数字列表,为待求数组。假设上一行数组为 [1,1],即第二行数字。那么,下一行数组的元素值就等于上一行相邻两个数字的和,即为 2,然后数组两端的值为 1,这样就可以求出下一行数组,即第三行数字列表。求第四行数组的值,可以把已计算出的第三数组作为上一行数组,而第四行数字为待求的下一行数组,以此类推。实现代码
使用嵌套循环结构,外层循环遍历高次方的幂数(即行数),内层循环遍历每次方的项数(即列数)。具体代码如下:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | function print(v){if (typeof v == "number") { var w = 30; if(n>30) w = (n-30) + 40; var s = '<span style="padding:4px 2px;display:inline-block;text-align:center;width:' + w + 'px;">'+v+'</span>'; document.write(s);}else{ document.write(v);}}var n = prompt("请输入幂数:",9);n = n - 0;var t1 = new Date();var a1 = [1,1];var a2 = [1,1];print('<div style=text-align:center;">');for (var i = 0;i <=n;i++){ for (var j = 1; j < i + 2; j++) { print(c(i,j));}print("<br />");}print("</div>");var t2 = new Date();print("<p style='text-align:center;'>耗时为(毫秒):"+(t2-t1)+"</p>");function c(x,y){ if ((y == 1) || (y == x + 1)) return 1; return c(x-1,y-1) + c(x-1,y);} |

